Advanced Course: Combinatorial Convexity (May 7-18, 2012)
Combinatorics, Graph Theory and Applications
Doctoral Program on Applied Mathematics
Universitat Politècnica de Catalunya

Advanced Course
Combinatorial Convexity
by Imre Bárány
May 7-18, 2012
-
Course Description
-
Imre Bárány
-
Registration and further information
-
Schedule
-
Preliminary list of participants
-
Lecture room and directions
Course Description
Some literature:
- the classic survey by Danzer, Grunbaum, Klee "Helly's theorem and its relatives", Convexity, Proc. Symp. Pure Math., 7, American Mathematical Society, pp. 101–179.
- some chapters from J. Matousek's excellent book "Lectures on discrete geometry" Springer GTM Vol. 212, 2002.
Imre Bárány
Registration and further information
Please send an e-mail tagged 'Barany2012Course' to convexitycourse2012@ma4.upc.edu indicating
Name
Affiliation
e-mail address
Short cv (academic degree, current situation, mathematical background)
There is no registration fee.
For further information please contact convexitycourse2012@ma4.upc.edu.Poster announcement of the course.
Schedule
| Monday May 7 | 10h Welcome coffee (room 'R', FME) 11h-13h |
||
| Tuesday May 8 | 11h-13h | Tuesday May 15 | 11h-13h |
| Wednesday May 9 | 11h-13h | Wednesday May 16 | 11h-13h |
| Thursday May 10 | 11h-13h | Thursday May 17 | 11h-13h |
| Friday May 11 | 11h-13h |
Preliminary list of participants
Aguiló, Francesc (Ma4, UPC Barcelona)
Balbuena, Camino (UPC, Barcelona)
Ball, Simeon (Ma4, UPC, Barcelona)
Boroczky, Karoly (Renyi Institute Budapest)
Brunat, Josep M. (Ma2, UPC, Barcelona)
Comellas, Francesc (Ma4, UPC, Barcelona)
Dalfó, Cristina (Ma4, UPC, Barcelona)
Fàbrega, Josep (Ma4, UPC, Barcelona)
Fiol, Miquel Àngel (Ma4, UPC, Barcelona)
Hansberg, Adriana (UPC, Barcelona)
Huemer, Clemens (Ma4, UPC, Barcelona)
Lladó, Anna (Ma4, UPC, Barcelona)
López-Masip, Susana-Clara (Ma4, UPC, Barcelona)
Magazinov, Alexander (Mathematical Institute of RAS, Moscow)
Maureso, Montserrat (Ma2, UPC, Barcelona)
Miralles, Alícia (Ma4, UPC, Barcelona)
Molina, Enrique (UPC, Barcelona)
Mora, Mercè (Ma2, UPC Barcelona)
Padrol, Arnau (Ma2, UPC, Barcelona)Pelayo, Ignacio (Ma3, UPC Barcelona)
Perarnau, Guillem (Ma4, UPC, Barcelona)
Pérez-Mansilla, Sónia (Ma4, UPC, Barcelona)
Pfeifle, Julian (Ma2, UPC, Barcelona)
Petridis, Giorgis (Cambridge University)
Serra, Oriol (Ma4, UPC, Barcelona)
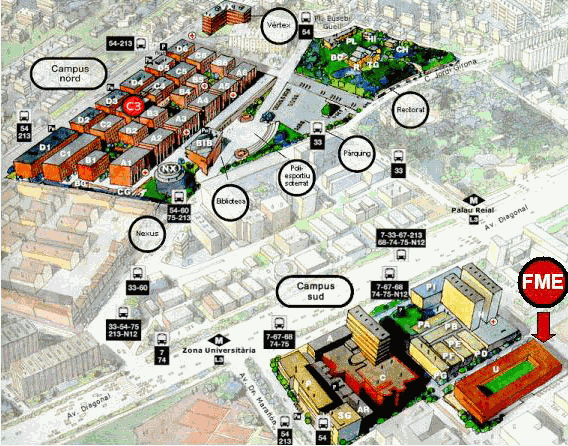
Lecture room and directions
The lectures will be held in Room 100 in the building of the Facultat de Matemàtiques i Estadística (FME).
Please see the map for the location of the building. To get there you can use Metro L3 (Green Line)
and step off at Palau Reial. For further directions ask info.osrm@upc.edu.
Updates will be posted concerning lecture room, directions, list of participants and course notes.
Share: